Activité 1 : Je manipule les pyramides
TEMPS 1 : Entrer dans la géométrie dans l'espace
-
Voici trois pyramides, pour chacune, indique :
- son sommet
- sa base
- une arête latérale
- une face latérale cachée.
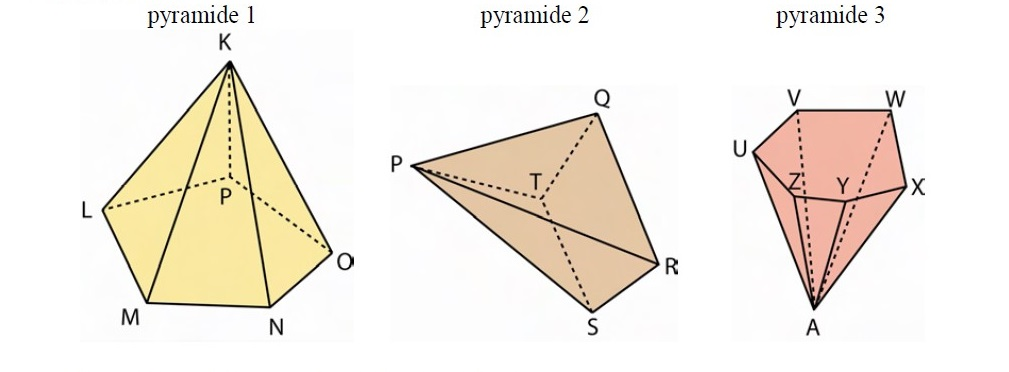
- Complète le tableau suivant :

- Que remarque-t-on concernant le nombre de sommets, de faces et d’arêtes de chaque pyramide ? Quelles conjectures peut-on émettre ? (Rappel : une conjecture est une supposition, une chose qui nous semble vraie mais pour laquelle nous n’avons pas de preuve)
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
TEMPS 2 : Essayons de voir si ces conjectures sont vraies, c’est-à-dire savoir si elles « marchent » pour n’importe quelle pyramide.
- Détermine le nombre de sommets, de faces et d’arêtes pour une pyramide dont la base a 10 sommets.
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
- Nous allons maintenant imaginer une pyramide dont la base a n sommets. Détermine le nombre S de sommets, le nombre F de faces, le nombre A d’arêtes de cette pyramide. Explique avec des phrases ton raisonnement. Tu peux également t’aider de schémas.
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………………
Que peut-on conclure ?
……………………………………………………………………………………………………………………………………………………………………………

